ねらい 等式を天秤のつりあいにたとえて方程式の解き方を考え 等式の性質を理解する Ppt Download
数学・算数 私は高校1年生です。 最近になって不等式がさっぱりわからなくなってしまい困っています。 不等式の解き方を教えてください。 できるだけ分かりやすく教えていただけた等式の変形で 解き方を説明してくれませんか？ Clearnote 解き方を説明してくれませんか？ 分数などが含まれている等式が苦手です。 記 次の等式を, 〔 内の文字について解きなさい。 回 (1)
等式 解き方 yについて
等式 解き方 yについて- 中2数学「等式の変形の解き方と練習問題」 中2数学「等式の変形」方程式のように解くことがポイント！ についてまとめています。 等式の変形は、中学1年生で学習した「一次方程式 解き方や応用問題（文章題、絶対値や分数） 二次不等式とは？解き方や解の範囲の求め方、判別式の問題 準備数直線の書き方 連立不等式を解くにあたって、数直線の書き方を簡単
中学数学 連立方程式 文章題の解き方 立式のコツ
次に、連立二次不等式の解き方について説明します。 問題以下の2つの2次不等式を満たすxの範囲を求めなさい。 x²5x4≧0① x²5x≦0② 解説 基本は二次不等式と同じで、ま 等式の変形のやり方がわかる3つのステップ つぎの練習問題をときながら解き方をみていこう。 練習問題 つぎの等式を 内の文字について解きなさい。 12a 5b = 2 (4a1) a 等式の変形はつぎの3ステップでとけちゃうんだ。 Step1 分配法則をつかって等式 2xy=5 を y について解きなさい。 これは、どうやって解いたらいいんですか？ 解き方教えてください。 0 回答 ゆっち 6年弱前 まずはじめに「yについて解く」の言葉の意味を確認しますね。「yについて解く」はつまり"y= "の形にするということです。(ちなみにxについて解くと言われれば
等式の変形 等式 xy=5 を x=5 y に変形したり， S= ah2nn を h= 2Sann に変形することは， 次に習う方程式の解き方において基本となる技術です． 例題 分数の方程式の解き方！分母を消せば中1の子でも絶対解ける！ ・次の等式を 内の文字について解いてみよう。 このような文字について解く問題は、まず左辺に目的の文字をもっ さらに、等式の性質をもとにしたやり方である「 移項 」も、等式の変形を解いていく上で必要になります。 移項とは、 一方の辺にある項を、 符号を逆にして もう一方の辺に移動させ
等式 解き方 yについてのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 等式の変形 図形の関係式を変形する 教遊者 | 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
 等式の変形 図形の関係式を変形する 教遊者 | 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
 等式の変形 図形の関係式を変形する 教遊者 | 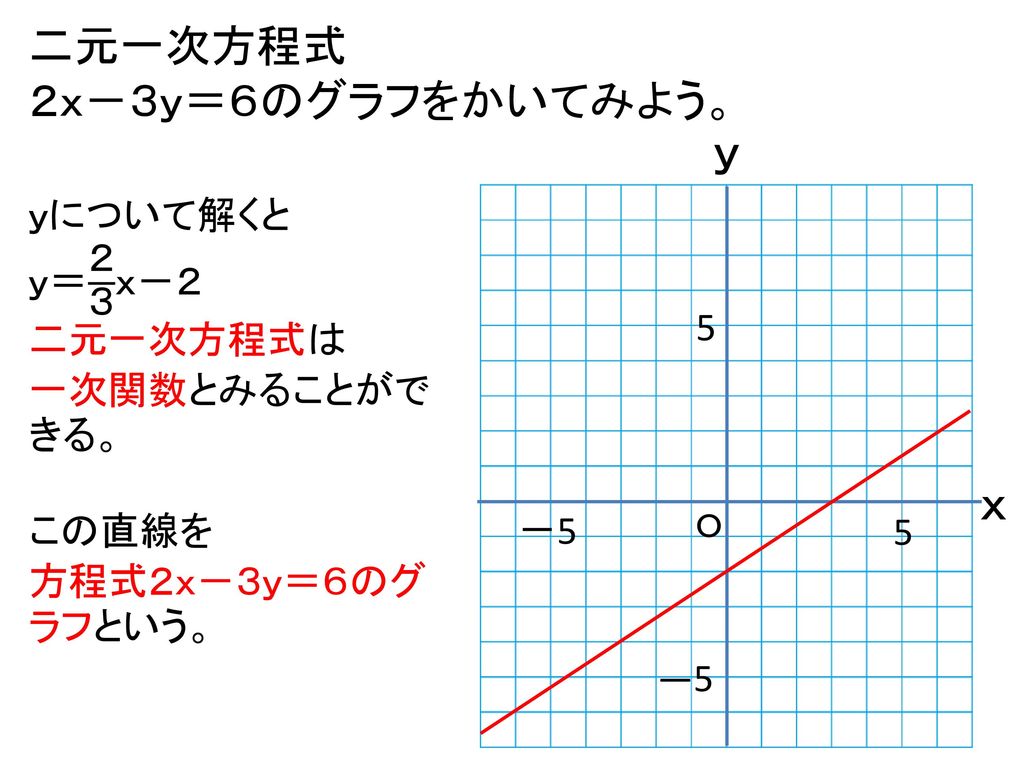 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |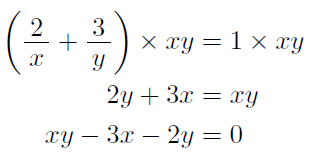
 等式の変形 図形の関係式を変形する 教遊者 | 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
 等式の変形 図形の関係式を変形する 教遊者 | 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
 等式の変形 図形の関係式を変形する 教遊者 | 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 | 等式の変形 図形の関係式を変形する 教遊者 |
 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
等式の変形 図形の関係式を変形する 教遊者 | 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
 等式の変形 図形の関係式を変形する 教遊者 | 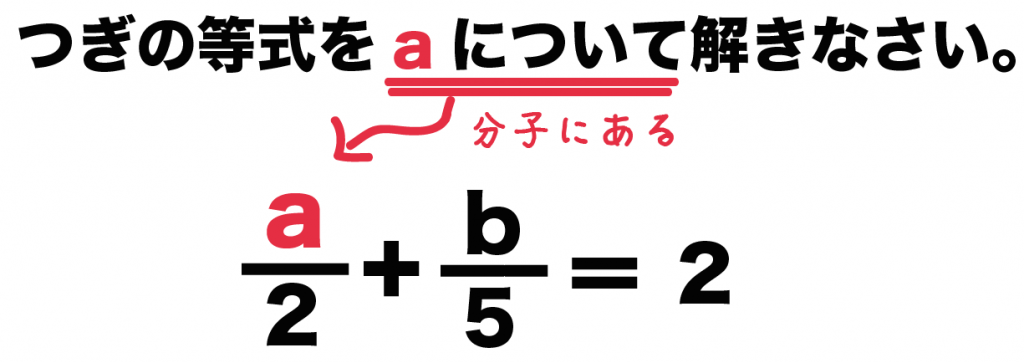 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |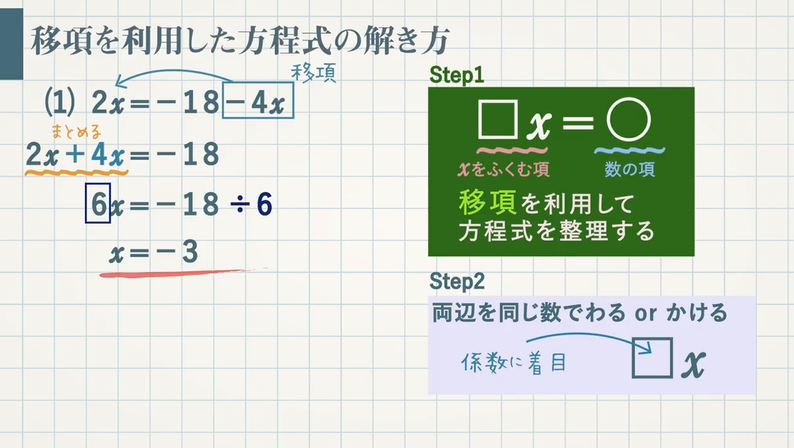
 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |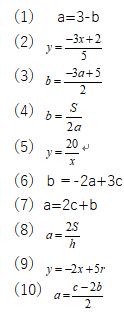
 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |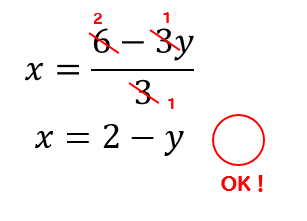
等式の変形 図形の関係式を変形する 教遊者 | 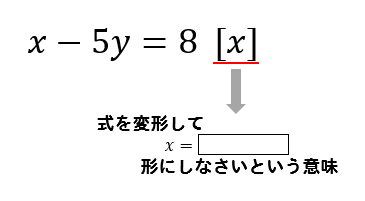 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |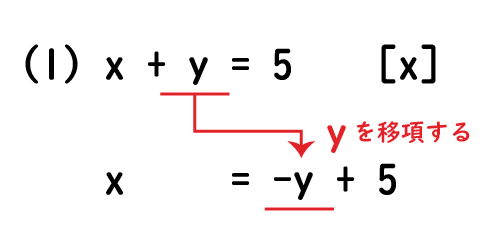
 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |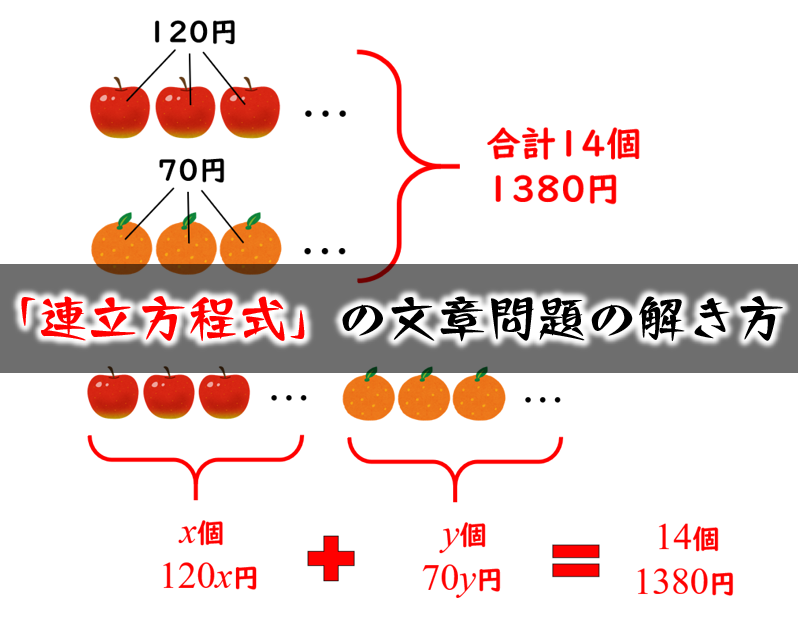
 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |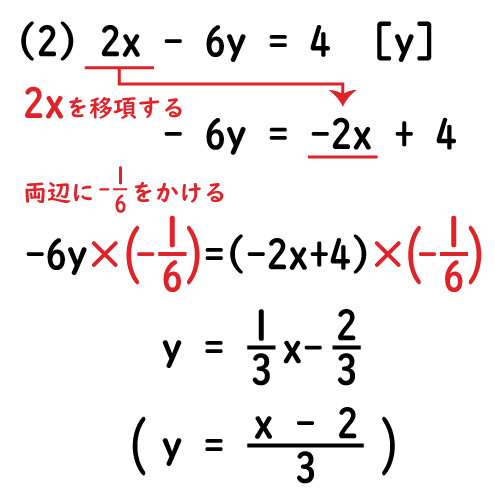
等式の変形 図形の関係式を変形する 教遊者 |  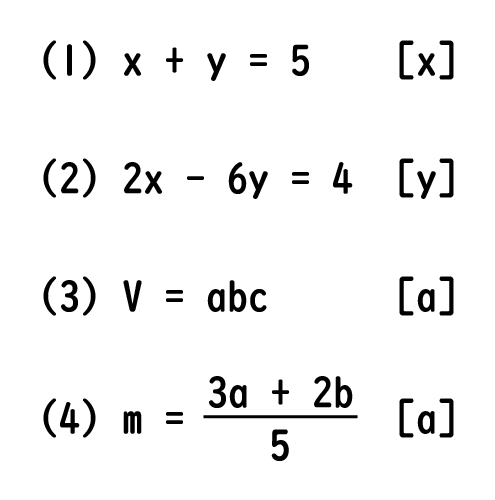等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
 等式の変形 図形の関係式を変形する 教遊者 | 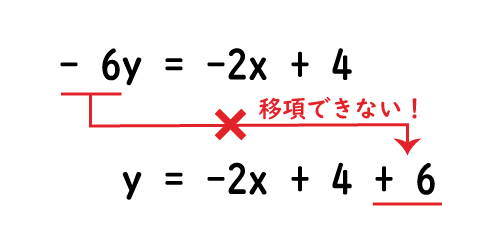 等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
等式の変形 図形の関係式を変形する 教遊者 |  等式の変形 図形の関係式を変形する 教遊者 |
例題 $ y=axb $ を $ a $ について解き なさい。 解き方 1次関数の変化の割合(傾き)について求める問題です。 $ y=axb $ 左辺と右辺を入れ替えても同じですので、考えやすいように左辺と式と方程式について掘り下げて解説してきました。 ここまでの話をまとめていくと、数学の問題として出てくる「式」と「方程式」の違いとは、 形 計算のゴール の2点です。 形としては、式の場合
Incoming Term: 等式 解き方 yについて,
0 件のコメント:
コメントを投稿